Comptonin ilmiö

Comptonin ilmiö on seuraus sähkömagneettisen säteilyn dualistisesta luonteesta. Käytännössä ilmiö tarkoittaa sitä, että säteily törmää vapaaseen elektroniin ja syntyvässä täysin kimmoisessa törmäyksessä säteily luovuttaa osan energiastaan elektronin liike-energiaksi. Comptonin ilmiölle voidaan johtaa kaava dL = (1 - cos a) * h/(mc), missä:
- dL on säteilyn aallonpituuden muutos
- a on siroamiskulma
- h on Planckin vakio (6.626076 * 10^-34 Js)
- m on elektronin lepomassa (9.1093895 * 10^-31 kg)
- c on valon nopeus tyhjiössä (2.99792458 * 10^8 m/s)

Piirretään tilanteesta kuva:

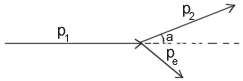
Tässä p1 on säteilyn (fotonin) liikemäärä alussa ja p2 on sen liikemäärä lopussa. pe on elektronin liikemäärä törmäyksen jälkeen. Siirretään vektorit siten, että saadaan muodostettua seuraavanlainen kolmio:

Voidaan kirjoittaa kaksi yhtälöä, sillä täysin kimmoisassa törmäyksessä sekä energia, että liikemäärä säilyvät.
Energia säilyy: E1 + Ee1 = E2 + Ee2 (1)
Liikemäärä säilyy: p1 = p2 + pe (huom. liikemäärä on vektorisuure!)

Vektoreista päästään välittömästi eroon soveltamalla kosinilausetta yllä olevaan kolmioon:
pe^2 = p1^2 + p2^2 - 2 p1 p2 cos a (2)

Ennen törmäystä elektronin kokonaisenergia voidaan lausua Ee1 = mc^2. Törmäyksen jälkeen elektronilla on kuitenkin liike-energiaa, joten tulee käyttää kokonaisenergian kaavaa: Ee2 = c*sqrt[pe^2 + (mc)^2] (huom. m on näissä elektronin lepomassa!)

Säteilykvantille pätee kaava p = h/L = E/c. Tästä saadaan E1 = hc/L1 ja E2 = hc/L2
Yhtälö 1 voidaan siis kirjoittaa muotoon hc(1/L1 - 1/L2) = c*sqrt[pe^2 + (mc)^2] - mc^2

Tässä on edelleen tuntematon suure pe, joka voidaan ratkaista yhtälöstä 2:
pe^2 = h^2(1/L1^2 + 1/L2^2 - 2 cos a/(L1 L2))

Sijoittamalla saadaan:
hc(1/L1 - 1/L2) = c*sqrt[h^2(1/L1^2 + 1/L2^2 - 2 cos a/(L1 L2)) + (mc)^2] - mc^2 (ryhmitellään)
h(1/L1 - 1/L2) + mc = sqrt[h^2(1/L1^2 + 1/L2^2 - 2 cos a/(L1 L2)) + (mc)^2] (korotetaan puolittain toiseen)
h^2(1/L1^2 + 1/L2^2) + (mc)^2 - 2h^2/(L1 L2) - 2hmc/L2 + 2hmc/L1) = h^2(1/L1^2 + 1/L2^2 - 2 cos a/(L1 L2)) + (mc)^2
1/L1^2 + 1/L2^2 - 2/(L1 L2) - 2mc/(hL2) + 2mc/(hL1) = 1/L1^2 + 1/L2^2 - 2 cos a/(L1 L2)
- 2/(L1 L2) - 2mc/(hL2) + 2mc/(hL1) = - 2 cos a/(L1 L2) (kerrotaan puolittain termillä (L1 L2)/(-2)
1 + mcL1/h - mcL2/h = cos a
1 - cos a = mc/h(L2 - L1)
dL = (1 - cos a) * h/(mc)

Johdetaan kokonaisenergian kaava:
Lähdetään liikkeelle kaavasta E = mc^2.
E = mvc^2 (tässä m on liikemassa, korotetaan neliöön)
E^2 = (mvc^2)^2
E^2 = m^2 c^4/(1 - v^2 / c^2)
E^2 (1 - v^2 / c^2) = m^2 c^4
E^2 (1 - v^2 / c^2)  = m^2 c^4 + m^2 c^2 v^2 - m^2 c^2 v^2
E^2 (1 - v^2 / c^2) = m^2 c^4 (1 - v^2 / c^2) + m^2 c^2 v^2
E^2 = m^2 c^4 + m^2 c^2 v^2 / (1 - v^2 / c^2)
E^2 = m^2 c^4 + c^2 p^2
E = c * sqrt(p^2 + (mc)^2)